本文共 6157 字，大约阅读时间需要 20 分钟。
通过上一小节，我们基于对称矩阵的重要性质以及主成分分析中的几何原理，带领大家从头到尾认认真真的推导了一遍奇异值分解的过程，明确了其中各个成分矩阵的求解方法和来龙去脉，相信此时大家已经牢固的掌握了奇异值分解相关的理论基础和思想方法。那么，我们具体应该如何运用这个有力武器对数据进行降维处理呢？这就是本节要讲述的关键问题。
奇异值分解的精彩之处在于，他可以从行和列这两个不同的维度同时展开对数据的降维处理工作。一个采样数据矩阵的行和列通常代表着不同的特征，因此奇异值分解的这种特性可以带来非常便捷的处理效果。
同时，本节还会借鉴级数的思想，介绍如何从整体的角度如何对一个矩阵进行近似处理，并和大家一起利用Python工具来实践这些想法，为第6章的实践与应用打好基础。
5.5.1 行压缩数据降维在这里，我们直接从矩阵A的奇异值分解式子：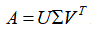
入手，分析如何进行行压缩数据降维。
我们将等式两侧同时乘以左奇异矩阵的转置矩阵：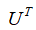
，得到：
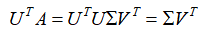，注意，重点是左侧的表达式
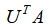，我们把矩阵A记作n个m维列向量并排放置的形式，我们展开来看：
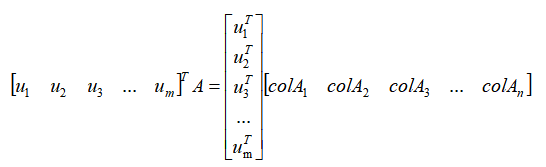
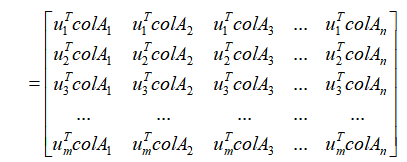
这是我们刚刚讲过的基变换方法，大家应该很熟悉了吧，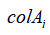
原本使用的是默认的一组基向量
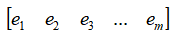，我们通过应用上面的基变换，将其用
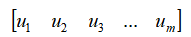这一组标准正交基来表示，由于这一组标准正交基本质上也是由协方差对称矩阵
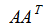得到，因此将各列做基变换后，数据分布从行的角度来看就变得彼此无关了。
此时，我们可以把每一列看作是一个样本，各行是样本的不同特征，各行之间彼此无关，我们可以按照熟悉的方法，选择最大的k个奇异值对应的k个标准正交向量，形成行压缩矩阵：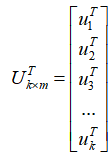
。
通过式子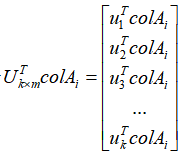
，就实现了列向量从m维到k维的数据降维，完成了主成分的提取。
奇异值分解的精彩之处就在于他可以从两个维度进行数据降维，分别对其提取主成分，前面介绍的是对行进行压缩降维，那么下面我们来说说如何对列进行压缩降维。
还是牢牢的抓住奇异值分解的分解表达式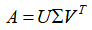
进行启发，我们对式子两边同时乘以右奇异矩阵V，就得到了等式
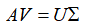，接下来，我们还是聚焦等式的左侧表达式：AV。
我们对其式子的整体进行转置的预处理，得到了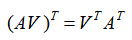
，我们把矩阵A记作
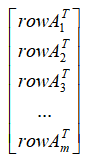，那么同样的道理有：
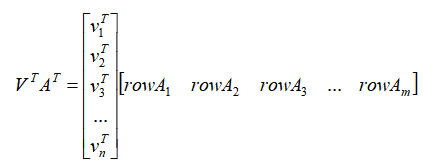
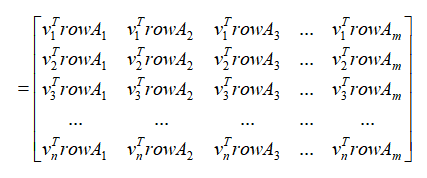
类比一下上面讲过的行压缩过程，在矩阵V中我们从大到小取前k个特征值所对应的标准正交特征向量，就构成了另一个压缩矩阵：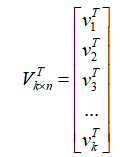
。很明显，通过乘法运算
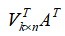就能够实现将
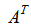矩阵的各列由n维压缩到k维的目的。而且，请大家不要忘记了，转置矩阵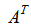的列不正是矩阵A的各行吗。
通过上面描述的过程，我们将各行向量的维数由n维压缩到了k维，顺利实现了列压缩的数据降维。
这里所介绍的从行压缩和列压缩两个方向上进行数据降维的处理手段在推荐系统中有非常强的实际应用价值，我们在最后一章会举例详细说明。
5.5.3 对矩阵整体进行数据压缩这里我们不谈按行压缩还是按列压缩，我们从矩阵的整体处理视角再介绍一个数据压缩的方式。在这里，我们的思路有点类似级数的概念，将一个m×n的原始数据矩阵A分解成若干个同等维度矩阵乘以各自权重后相加的形式。这种处理思想在高等数学中经常出现，那么在这里该如何实现呢？
同样的，还是依旧从奇异值分解的表达式入手，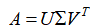
，我们将他展开成完整的矩阵形式：
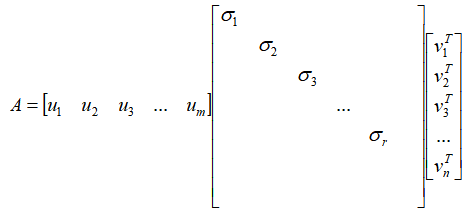，等式中的各个参数满足r≤n
这里将矩阵相乘的式子展开后就得到了：
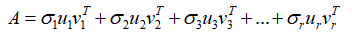
大家不难发现，展开式中每一个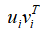
相乘的结果都是一个等维的m×n形状的矩阵，并且他们彼此之间都满足正交的关系，前面的系数
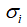则是各个对应矩阵的权重值。
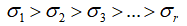的不等关系则依序代表了各个矩阵片段“重要性”的程度，因此我们可以按照主成分贡献率的最低要求选择前k个数据项进行叠加，用来对原始数据矩阵A进行近似处理：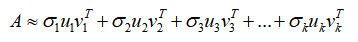
原理示意图如图5.9所示。
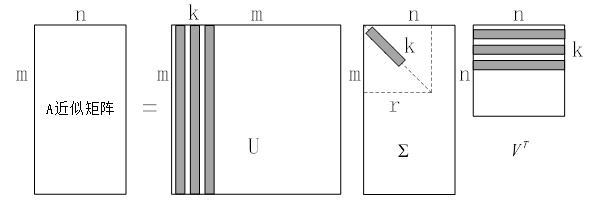
图5.9.利用数据压缩进行矩阵近似
这种思想和处理方式在图像压缩的应用中很有用处，我们在最后一章的实战章节中也会具体讲到。
5.5.4 利用Python进行奇异值分解我们以一个7×5的矩阵A为例，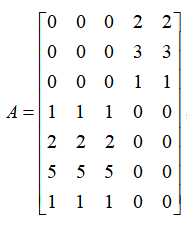
，这是一个看上去很有规律的矩阵。
我们这里就不按照推导奇异值分解原理的计算过程：先求对称矩阵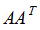
和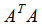
，再接着依次求取几个重要的矩阵U，V，
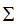，这样一步步的进行计算。我们通过Python语言提供的工具，直接一次性获得奇异值分解的所有成分结果。
代码如下：
import numpy as np A=[[0, 0, 0, 2, 2], [0, 0, 0, 3, 3], [0, 0, 0, 1, 1], [1, 1, 1, 0, 0], [2, 2, 2, 0, 0], [5, 5, 5, 0, 0], [1, 1, 1, 0, 0]] U, sigma, VT = np.linalg.svd(A) print(U) print(sigma) print(VT)
运行结果：
[[ 0.00000000e+00 5.34522484e-01 8.41650989e-01 5.59998398e-02 -5.26625636e-02 1.14654380e-17 2.77555756e-17] [ 0.00000000e+00 8.01783726e-01 -4.76944344e-01 -2.09235996e-01 2.93065263e-01 -8.21283146e-17 -2.77555756e-17] [ 0.00000000e+00 2.67261242e-01 -2.52468946e-01 5.15708308e-01 -7.73870662e-01 1.88060304e-16 0.00000000e+00] [ -1.79605302e-01 1.38777878e-17 7.39748546e-03 -3.03901436e-01 -2.04933639e-01 8.94308074e-01 -1.83156768e-01] [ -3.59210604e-01 2.77555756e-17 1.47949709e-02 -6.07802873e-01 -4.09867278e-01 -4.47451355e-01 -3.64856984e-01] [ -8.98026510e-01 5.55111512e-17 -8.87698255e-03 3.64681724e-01 2.45920367e-01 -6.85811202e-17 1.25520829e-18] [ -1.79605302e-01 1.38777878e-17 7.39748546e-03 -3.03901436e-01 -2.04933639e-01 5.94635264e-04 9.12870736e-01]] [ 9.64365076e+00 5.29150262e+00 7.40623935e-16 4.05103551e-16 2.21838243e-32] [[ -5.77350269e-01 -5.77350269e-01 -5.77350269e-01 0.00000000e+00 0.00000000e+00] [ -2.46566547e-16 1.23283273e-16 1.23283273e-16 7.07106781e-01 7.07106781e-01] [ -7.83779232e-01 5.90050124e-01 1.93729108e-01 -2.77555756e-16 -2.22044605e-16] [ -2.28816045e-01 -5.64364703e-01 7.93180748e-01 1.11022302e-16 -1.11022302e-16] [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 -7.07106781e-01 7.07106781e-01]]
这样我们就非常简单的一次性获得了奇异值分解的所有结果。
我们在这里需要强调一点的是，通过程序所获得的sigma变量不是一个矩阵，而是由5个奇异值按照从大到小顺序组成的一个列表。而分解过程中所得结果的最后一项，打印出来的不是V矩阵，而是转置后的矩阵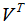
。
下面我们利用奇异值分解的结果来对数据进行行压缩和列压缩的操作实践：
我们观察这一组奇异值，我们发现前两个奇异值在数量级上占有绝对的优势，因此我们选择k=2进行行压缩和列压缩。
依照上面介绍的知识点，我们利用矩阵乘法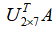
将矩阵A的行数由7行压缩成了2行。利用矩阵乘法
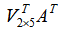，将矩阵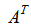的行由5行压缩成了2行，换句话说就是将矩阵A的列由5列压缩成了2列。
我们用Python代码来演示从行和列两个维度对矩阵
进行压缩的过程。
代码如下：
import numpy as np A=[[0, 0, 0, 2, 2], [0, 0, 0, 3, 3], [0, 0, 0, 1, 1], [1, 1, 1, 0, 0], [2, 2, 2, 0, 0], [5, 5, 5, 0, 0], [1, 1, 1, 0, 0]] U, sigma, VT = np.linalg.svd(A) U_T_2x7 = U.T[:2,:] print(np.dot(U_T_2x7,A)) VT_2x5=VT[:2,:] print(np.dot(VT_2x5,np.mat(A).T).T)
运行结果：
[[ -5.56776436e+00 -5.56776436e+00 -5.56776436e+00 0.00000000e+00 0.00000000e+00] [ 3.60822483e-16 3.60822483e-16 3.60822483e-16 3.74165739e+00 3.74165739e+00]] [[ 0.00000000e+00 2.82842712e+00] [ 0.00000000e+00 4.24264069e+00] [ 0.00000000e+00 1.41421356e+00] [ -1.73205081e+00 -7.39557099e-32] [ -3.46410162e+00 -1.47911420e-31] [ -8.66025404e+00 -2.95822839e-31] [ -1.73205081e+00 -7.39557099e-32]]
通过代码运行的结果进行总结：我们成功的分别对矩阵A的行和列进行了压缩，行压缩后的结果矩阵是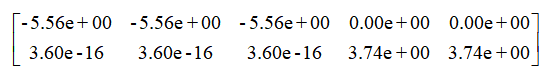
，列压缩的结果矩阵是
。
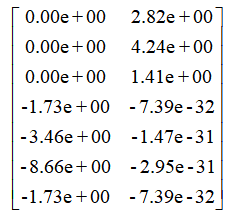最后，我们来实践一下如何对矩阵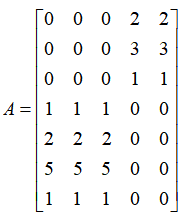
从整体维度上进行数据压缩。同样，我们取前两个主成分贡献率高的奇异值
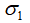和
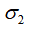，利用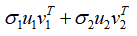
进行矩阵A的近似。
代码如下：
import numpy as np A=[[0, 0, 0, 2, 2], [0, 0, 0, 3, 3], [0, 0, 0, 1, 1], [1, 1, 1, 0, 0], [2, 2, 2, 0, 0], [5, 5, 5, 0, 0], [1, 1, 1, 0, 0]] U, sigma, VT = np.linalg.svd(A) A_1 = sigma[0]*np.dot(np.mat(U[:, 0]).T, np.mat(VT[0, :])) A_2 = sigma[1]*np.dot(np.mat(U[:, 1]).T, np.mat(VT[1, :])) print(A_1+A_2)
运行结果：
[[ -6.97395509e-16 3.48697754e-16 3.48697754e-16 2.00000000e+00 2.00000000e+00] [ -1.04609326e-15 5.23046632e-16 5.23046632e-16 3.00000000e+00 3.00000000e+00] [ -3.48697754e-16 1.74348877e-16 1.74348877e-16 1.00000000e+00 1.00000000e+00] [ 1.00000000e+00 1.00000000e+00 1.00000000e+00 5.19259273e-17 5.19259273e-17] [ 2.00000000e+00 2.00000000e+00 2.00000000e+00 1.03851855e-16 1.03851855e-16] [ 5.00000000e+00 5.00000000e+00 5.00000000e+00 2.07703709e-16 2.07703709e-16] [ 1.00000000e+00 1.00000000e+00 1.00000000e+00 5.19259273e-17 5.19259273e-17]]
从程序最终的运行结果来看，我们得到的近似矩阵为
，这个矩阵的左上角和右下角的矩阵块，实质上都是约等于0的极小量，因此，我们将该求得的近似矩阵和原矩阵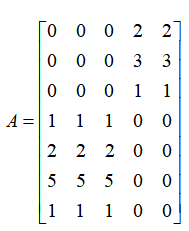
进行对比发现基本上是一致的。由此可以说我们利用上述方法，利用较少的数据量实现了不错的矩阵近似效果。
希望大家能通过本章的学习，深刻的理解数据降维和主成分分析的理论知识，并且熟练的利用Python工具进行相关操作。我们在最后一章会利用这些有力武器来解决几个实际的有趣问题。
▼往期精彩回顾▼前言1.1 描述空间的工具：向量1.2 基底构建一切，基底决定坐标1.3 矩阵，让向量动起来1.4 矩阵乘向量的新视角：变换基底2.1 矩阵：描述空间中的映射2.2 追因溯源：逆矩阵和逆映射3.1 投影，寻找距离最近的向量3.2 深入剖析最小二乘法的本质3.3 施密特正交化：寻找最佳投影基地4.1相似变换：不同的视角，同一个变换4.2 对角化：寻找最简明的相似矩阵4.3 关键要素：特征向量与特征值5.1 最重要的矩阵：对称矩阵
5.2 数据分布的度量
5.3利用特征值分解进行主成分分析(PCA)
5.4 更通用的利器：奇异值分解(SVD)
本书所涉及的源代码已上传到百度网盘，供读者下载。请读者关注封底“ 博雅读书社”微信 公众号，找到“ 资源下载”栏目，根据提示获取。 
如果您对本书感兴趣，请进入当当网选购！
转载地址：http://ewtdy.baihongyu.com/